Example:
Let’s understand the minimum spanning tree with an example.
So, as we know, the minimum spanning tree is a part of the graph but with less cost. So this scenario can be illustrated with an example.
Let’s suppose we have a graph like this.
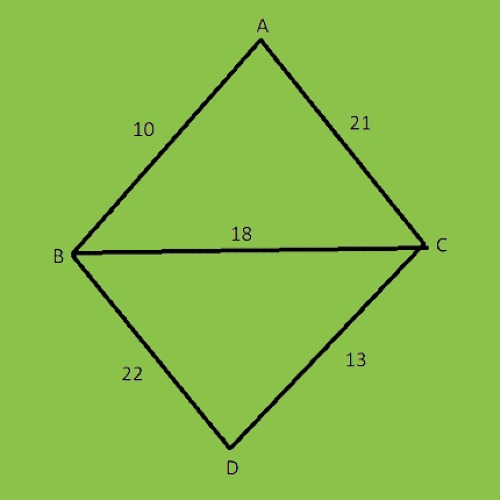
The above graph can be arranged in different ways so that the graph cycle will be removed, or else it will not be an MST (minimum spanning tree). So we will remove the cycle from the graph and count the total cost of the graph. We have four nodes, or vertices (A, B, C, and D).
Case – 1:
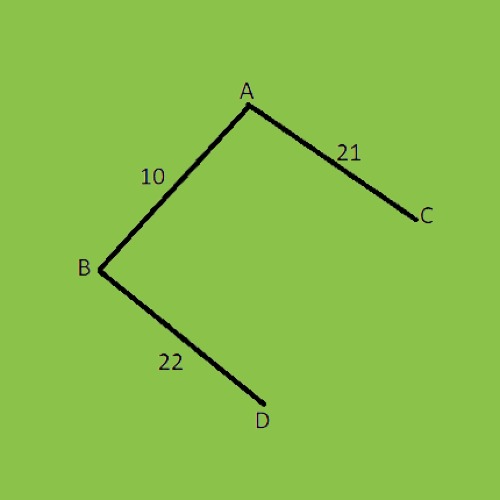
After removing the cycle from the graph, the above MST (minimum spanning tree) graph cost is 56.
Case -2:
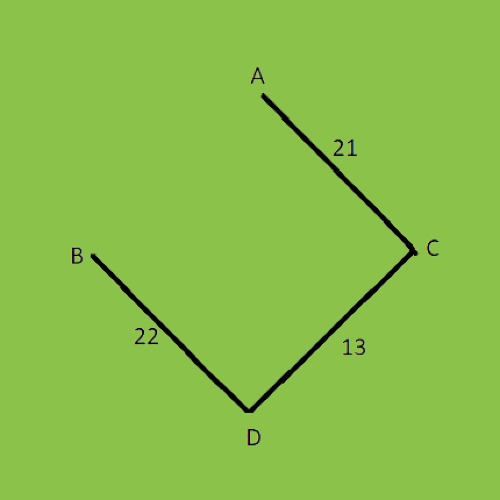
After removing the cycle from the graph, the above MST (minimum spanning tree) graph cost is 53.
Case – 3:
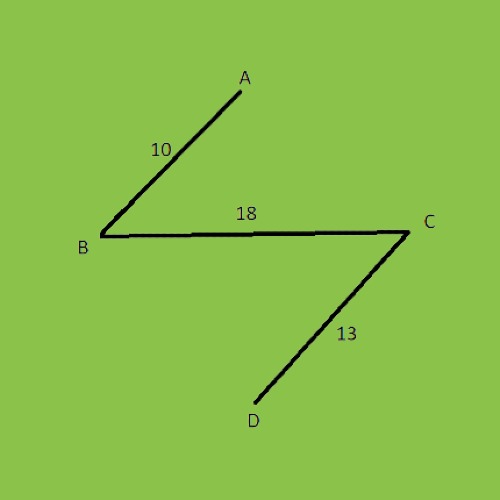
After removing the cycle from the graph, the above MST (minimum spanning tree) graph cost is 41.
We can see that the last graph of case-3’s total cost is much lower compared to the other two graphs. So this graph is our final MST (minimum spanning tree) for the original graph. The Prim’s or Kruskal’s algorithms’ motive is to find the graph cost as low as possible. So that’s our motive in this article to explain this MST.
We can draw a spanning tree with the help of the following two methods:
1. Kruskal’s algorithm
2. Prim’s algorithm
In this article, we are going to discuss Kruskal’s algorithm. Prim’s algorithm will be discussed in the next article.
Kruskal’s Algorithm:
Kruskal’s algorithm is very easy to implement compared to Prim’s algorithm because we don’t have to care about the adjacency vertices in this algorithm. In this algorithm, Kruskal’s algorithm starts from all the vertices of the graph. We choose the minimum weight edge vertice and start creating the minimum spanning tree. We choose another edge with the minimum weight and add it to the minimum spanning tree. This process continues until we do not add all the original graph nodes. Once all the nodes in the graph are added to the minimum spanning tree, the algorithm will stop. During creating the minimum spanning tree of a graph, we also have to take care of that graph, not creating any cycles because cycles should not be in the minimum spanning tree.
So, if any node creates the cycle in the minimum spanning tree, we choose the other node, even if this node’s weight is greater than the previous node that creates the cycle.
Kruskal’s algorithm is different from Prim’s algorithm. Prim’s algorithm, while creating a minimum spanning tree, starts from any node or vertice and then adds another node or vertice only from the adjacency nodes. But Kruskal’s algorithm does not care about the adjacency node and always selects that node that has less weight, but that node should not create a cycle in the minimum spanning tree.
Kruskal’s Algorithm Steps:
The following steps are taken while writing the C++ code for Kruskal’s algorithm.
Step 1: We create an array to store groups of the nodes or vertices of the graph.
Step 2: We create another array to store graph edges weights.
Step 3: For the spanning tree, we create a new array.
Step 4: We arrange the edges array in ascending order.
Step 5: We repeat step 6 until the array of sorted edge weights is not empty.
Step 6: We compare the two groups side by side. In this case, if one node of a group does not match the other node, we add that edge to the spanning tree and add it into the same group.
Step 7: Iterate through all of the spanning tree’s edges to determine its total weight.
Example:
Now, we will implement the above algorithm steps using an example. We have the below graph, and we will find out the minimum spanning tree for this graph.
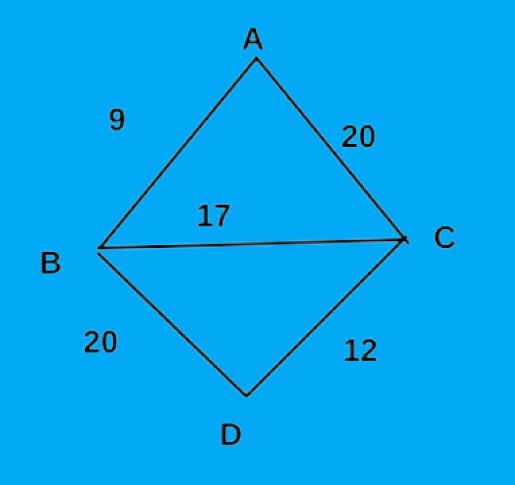
So, according to the algorithm, we first choose the smallest weight edge, which is AB. So we chose that edge and kept it in the spanning tree array. The weight of the AB edge is 9.
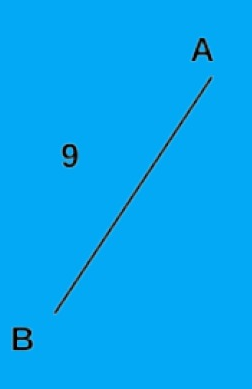
Now, we choose the next smallest weight edge, CD, and keep that edge in the minimum spanning tree array. The CD edge weight is 12.
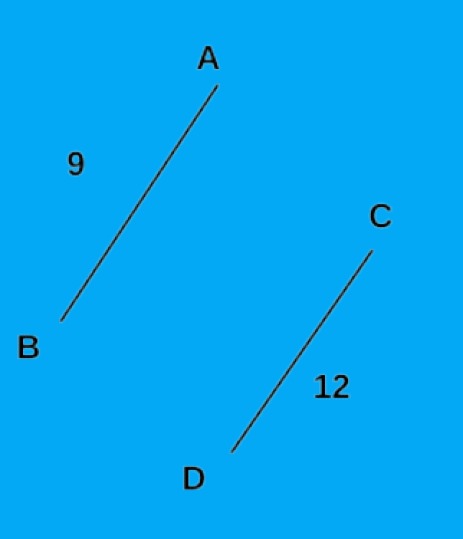
The next smallest edge we got was BC, which we kept in the array. The weighted BC edge is 17.
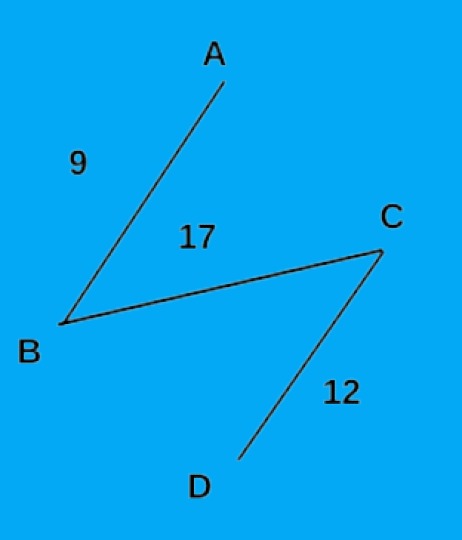
Our algorithm will stop here because we have all the vertices of a graph, and we have got our minimum spanning tree. The total weight of this MST is 9 + 12 + 17 = 38.
Program: The below is a C++ code for Kruskal’s algorithm.
#include
#include
class EdgeGraph {
public:
int nodeSTART;
int nodeEND;
int wght;
EdgeGraph(){}
EdgeGraph(int node_1, int node_2, int weight): nodeSTART(node_1),
nodeEND(node_2), wght(weight){}
};
bool CompareEdgeCost (const EdgeGraph a, const EdgeGraph b) {
return a.wght < b.wght;
}
class G{
private:
int num_of_nodes;
std :: vector EdgeGraphlist;
std :: vector parentNode;
std :: vector rankNode;
public:
G(){}
G (int num_of_nodes)
{
this->num_of_nodes = num_of_nodes;
parentNode.resize(num_of_nodes);
rankNode.resize(num_of_nodes);
}
void AddEdgeGraph(EdgeGraph e);
int FindparentNode(int node);
void KruskalMST_ALGO(std :: vector&);
void DisplayEdgeGraphs(std :: vector&);
};
void G :: AddEdgeGraph (EdgeGraph e) {
EdgeGraphlist.push_back(e);
}
int G :: FindparentNode (int node) {
if ( node != parentNode[node] )
parentNode[node] = FindparentNode(parentNode[node]);
return parentNode[node];
}
void G :: DisplayEdgeGraphs (std :: vector& mst) {
int cost = 0;
std :: cout << "EdgeGraphs of MST : ";
for (auto& e : mst) {
std :: cout << "[" << e.nodeSTART << "-" << e.nodeEND
<< "](" << e.wght << ") ";
cost += e.wght;
}
std :: cout << "\n Kruskal MST Cost : " << cost << std :: endl;
}
//This is the main Kruskal's algorithm function which search
// the minimum spanning tree.
void G :: KruskalMST_ALGO (std :: vector& result) {
for (int i=0; i<num_of_nodes; i++) {
parentNode[i] = i;
rankNode[i] = 0;
}
sort(EdgeGraphlist.begin(), EdgeGraphlist.end(),
CompareEdgeCost);
for (auto& e : EdgeGraphlist) {
int root_1 = FindparentNode(e.nodeSTART);
int root_2 = FindparentNode(e.nodeEND);
if (root_1 != root_2) {
result.push_back(e);
if (rankNode[root_1] < rankNode[root_2]) {
parentNode[root_1] = root_2;
rankNode[root_2]++;
} else {
parentNode[root_2] = root_1;
rankNode[root_1]++;
}
}
}
}
int main() {
int num_of_nodes = 6; // (0, 1, 2, 3, 4, 5)
EdgeGraph e1(0, 1, 4);
EdgeGraph e2(0, 2, 1);
EdgeGraph e3(0, 3, 5);
EdgeGraph e4(1, 3, 2);
EdgeGraph e5(1, 4, 3);
EdgeGraph e6(1, 5, 3);
EdgeGraph e7(2, 3, 2);
EdgeGraph e8(2, 4, 8);
EdgeGraph e9(3, 4, 1);
EdgeGraph e10(4, 5, 3);
G g1(num_of_nodes);
g1.AddEdgeGraph(e1);
g1.AddEdgeGraph(e2);
g1.AddEdgeGraph(e3);
g1.AddEdgeGraph(e4);
g1.AddEdgeGraph(e5);
g1.AddEdgeGraph(e6);
g1.AddEdgeGraph(e7);
g1.AddEdgeGraph(e8);
g1.AddEdgeGraph(e9);
g1.AddEdgeGraph(e10);
std :: vector mst; // This will store the minimum spanning tree
g1.KruskalMST_ALGO(mst);
g1.DisplayEdgeGraphs(mst);
return 0;
}
Output:
| 1
2 |
EdgeGraphs of MST : [0-2](1) [3-4](1) [1-3](2) [2-3](2) [1-5](3)
Kruskal MST Cost : 9 |
Conclusion:
We have studied Kruskal’s minimum spanning tree, which is the first preference of most people when they have to find the MST graph from a graph. Kruskal’s algorithm is simple to grasp and implement in a real-world application. Like Prim’s algorithm, Kruskal’s algorithm is also very useful in real-life applications. So we must understand this algorithm.
from https://ift.tt/RKxZvBF




0 Comments