Illustration of Heap Data Structures
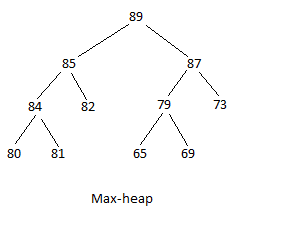
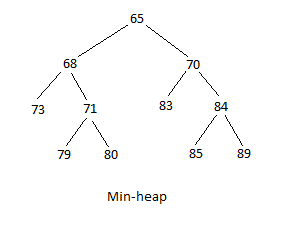
There are two types of heaps: a max-heap and a min-heap. A max-heap structure is where the maximum value is the root, and the values become smaller as the tree is descended; any parent is either equal to or bigger in value than either of its immediate children. A min-heap structure is where the minimum value is the root, and the values become bigger as the tree is descended; any parent is either equal to or smaller in value than either of its immediate children. In the following diagrams, the first is a max-heap and the second is a min-heap:
For both heaps, notice that for a pair of children, it does not matter whether the one on the left is the bigger value. A row in a level in the tree, must not necessarily be filled from minimum to maximum, from the left; it is not also necessarily filled from maximum to minimum, from the left.
Representing a Heap in an Array
For software to use a heap easily, the heap has to be represented in an array. The max-heap above, represented in an array is:
This is done beginning with the root value as the first value for the array. The values are continuously placed by reading the tree from left to right, from top to bottom. If an element is absent, its position in the array is skipped. Each node has two children. If a node is at index (position) n, its first child in the array is at index 2n+1, and its next child is at index 2n+2. 89 is at index 0; its first child, 85 is at index 2(0)+1=1 while its second child is at index 2(0)+2=2. 85 is at index 1; its first child, 84, is at index 2(1)+1=3 while its second child, 82 is at index 2(1)+2=4. 79 is at index 5; its first child, 65 is at index 2(5)+1=11 while its second child is at index 2(5)+2=12. The formulas are applied to the rest of the elements in the array.
Such an array, where the meaning of an element and the relationship between the elements, is implied by the position of the element, is called an Implicit Data Structure.
The implicit data structure for the above min-heap is:
The above max-heap is a complete binary tree but not a full binary tree. That is why some locations (positions) are empty in the array. For a full binary tree, no location will be empty in the array.
Now, if the heap were an almost complete tree, for example, if the value 82 was missing, then the array would be:
In this situation, three locations are empty. However, the formulas are still applicable.
Operations
A data structure is a format of data (e.g. a tree), plus the relationship among the values, plus the operations (functions) perform on the values. For a heap, the relationship that runs through the whole heap is, that the parent must be equal or greater in value than the children, for a max-heap; and the parent must be equal or less in value than the children, for a min-heap. This relationship is called the heap property. The operations of a heap are grouped under the headings of Creation, Basic, Internal and Inspection. A summary of the operations of the heap follows:
Heap Operations Summary
There are certain software operations that are common with heaps, as follows:
Creation of a Heap
create_heap: Creating a heap means forming an object that represents the heap. In the C language, you can create a heap with the struct object type. One of the members of the struct will be the heap array. The rest of the members will be functions (operations) for the heap. Create_heap means creating an empty heap.
Heapify: The heap array is a partially sorted (ordered) array. Heapify means, provide a heap array from an unsorted array – see details below.
Merge: This means, form a union heap from two different heaps – see details below. The two heaps should both be max-heap or both min-heap. The new heap is in conformity with the heap property, while the original heaps are preserved (not erased).
Meld: This means, join two heaps of the same type to form a new one, maintaining duplicates – see details below. The new heap is in conformity with the heap property, while the original heaps are destroyed (erased). The main difference between merging and melding is, that for melding, one tree fits as a subtree to the root of the other tree, allowing duplicate values in the new tree, while for merging, a new heap tree is formed, removing duplicates. There is no need to maintain the two original heaps with melding.
Basic Heap Operations
find_max (find_min): Locate the maximum value in the max-heap array and return a copy, or locate the minimum value in the min-heap array and return a copy.
Insert: Add a new element to the heap array, and rearrange the array so that the heap property of the diagram is maintained.
extract_max (extract_min): Locate the maximum value in the max-heap array, remove and return it; or locate the minimum value in the min-heap array, remove and return it.
delete_max (delete_min): Locate the root node of a max-heap, which is the first element of the max-heap array, remove it without necessarily returning it; or locate the root node of a min-heap, which is the first element of the min-heap array, remove it without necessarily returning it;
Replace: Locate the root node of either heap, remove it and replace it with a new one. It does not matter whether the old root is returned.
Internal Heap Operations
increase_key (decrease_key): Increase the value of any node for a max-heap and rearrange so that the heap property is maintained, or decrease the value of any node for a min-heap and rearrange so that the heap property is maintained.
Delete: delete any node, then rearrange, so that the heap property is maintained for the max-heap or a min-heap.
shift_up: move a node up in a max-heap or min-heap as long as needed, rearranging to maintain the heap property.
shift_down: move a node down in a max-heap or min-heap as long as needed, rearranging to maintain the heap property.
Inspection of a Heap
Size: This returns the number of keys (values) in a heap; it does not include the empty locations of the heap array. A heap can be represented by code, as in the diagram, or with an array.
is_empty: This returns Boolean true if there is no node in a heap, or Boolean false if the heap has at least one node.
Sifting in a Heap
There is sift-up and sift down:
Sift-Up: This means swap a node with its parent. If the heap property is not satisfied, swap the parent with its own parent. Continue this way in the path until the heap property is satisfied. The procedure might reach the root.
Sift-Down: This means swap a node of big value with the smaller of its two children (or one child for an almost complete heap). If the heap property is not satisfied, swap the lower node with the smaller node of its own two children. Continue this way in the path until the heap property is satisfied. The procedure might reach a leaf.
Heapifying
Heapify means sort an unsorted array to have the heap property satisfied for max-heap or min-heap. This means there might be some empty locations in the new array. The basic algorithm to heapify a max-heap or min-heap is as follows:
– if the root node is more extreme than either of its child’s node, then exchange the root with the less extreme child node.
– Repeat this step with the children nodes in a Pre-Order Tree Traversing Scheme.
The final tree is a heap tree satisfying the heap property. A heap can be represented as a tree diagram or in an array. The resulting heap is a partially sorted tree, i.e. a partially sorted array.
Heap Operation Details
This section of the article gives the details of the heap operations.
Creation of a Heap Details
create_heap
See above!
heapify
See above
merge
If the heap arrays,
and
are merged, the result without duplicates may be,
After some sifting. Notice that in the first array, 82 has no children. In the resulting array, it is at index 4; and its locations at index 2(4)+1=9 and 2(4)+2=10 are vacant. This means it also does not have children in the new tree diagram. The original two heaps should not be deleted since their information is not really in the new heap (new array). The basic algorithm to merge heaps of the same type is as follows:
– Join one array to the bottom of the other array.
– Heapify is eliminating duplicates, making sure that nodes which did not have children in the original heaps, still do not have children in the new heap.
meld
The algorithm for melding two heaps of the same type (either two max- or two min-) is as follows:
– Compare the two root nodes.
– Make the less extreme root and the rest of its tree (subtree), the second child of the extreme root.
– Sift the stray child of the root of now the extreme subtree, downwards in the extreme subtree.
The resulting heap is still in conformity with the heap property, while the original heaps are destroyed (erased). The original heaps can be destroyed because all the information they possessed is still in the new heap.
Basic Heap Operations
find_max (find_min)
This means to locate the maximum value in the max-heap array and return a copy, or locate the minimum value in the min-heap array and return a copy. A heap array by definition already satisfies the heap property. So, just return a copy of the first element of the array.
insert
This means add a new element to the heap array, and rearrange the array so that the heap property of the diagram is maintained (satisfied). The algorithm to do this for both types of heaps is as follows:
– Assume a full binary tree. This means the array has to be filled at the end with empty locations if necessary. The total number of nodes of a full heap is 1, or 3 or 7 or 15 or 31, etc.; keep doubling and adding 1.
– Put the node in the most suitable empty location by magnitude, towards the end of the heap (towards the end of the heap array). If there is no empty location, then start a new row from the bottom left.
– Sift up if necessary, until the heap property is satisfied.
extract_max (extract_min)
Locate the maximum value in the max-heap array, remove and return it; or locate the minimum value in the min-heap array, remove and return it. The algorithm to extract_max (extract_min) is as follows:
– Remove the root node.
– Take (remove) the bottom rightmost node (last node in the array) and place at the root.
– Sift down as appropriate, until the heap property is satisfied.
delete_max (delete_min)
Locate the root node of a max-heap, which is the first element of the max-heap array, remove it without necessarily returning it; or locate the root node of a min-heap, which is the first element of the min-heap array, remove it without necessarily returning it. The algorithm to delete the root node is as follows:
– Remove the root node.
– Take (remove) the bottom rightmost node (last node in the array) and place at the root.
– Sift down as appropriate, until the heap property is satisfied.
replace
Locate the root node of either heap, remove it and replace it with the new one. It does not matter whether the old root is returned. Sift down if appropriate, until the heap property is satisfied.
Internal Heap Operations
increase_key (decrease_key)
Increase the value of any node for a max-heap and rearrange so that the heap property is maintained, or decrease the value of any node for a min-heap and rearrange so that the heap property is maintained. Sift up or down as appropriate, until the heap property is satisfied.
delete
Remove the node of interest, then rearrange, so that the heap property is maintained for the max-heap or a min-heap. The algorithm to delete a node is as follows:
– Remove the node of interest.
– Take (remove) the bottom rightmost node (last node in the array) and place at the index of the node removed. If the node deleted is at the last row, then this may not be necessary.
– Sift up or down as appropriate, until the heap property is satisfied.
shift_up
Move a node up in a max-heap or min-heap as long as needed, rearranging to maintain the heap property – sift up.
shift_down
Move a node down in a max-heap or min-heap as long as needed, rearranging to maintain the heap property – sift down.
Inspection of a Heap
size
See above!
is_empty
See above!
Other Classes of Heaps
The heap described in this article can be considered as the main (general) heap. There are other classes of heaps. However, the two that you should know beyond this are the Binary Heap and the d-ary Heap.
Binary Heap
The binary heap is similar to this main heap, but with more constraints. In particular, the binary heap must be a complete tree. Do not confuse between a complete tree and a full tree.
d-ary Heap
A binary heap is a 2-ary heap. A heap where each node has 3 children is a 3-ary heap. A heap where each node has 4 children is a 4-ary heap, and so on. A d-ary heap has other constraints.
Conclusion
A heap is a complete or almost complete binary tree, that satisfies the heap property. The heap property has 2 alternatives: for a max-heap, a parent must be equal or greater in value than the immediate children; for a min-heap, a parent must be equal or less in value than the immediate children. A heap can be represented as a tree or in an array. When represented in an array, the root node is the first node of the array; and if a node is at index n, its first child in the array is at index 2n+1 and its next child is at index 2n+2. A heap has certain operations that are performed on the array.
Chrys
from Linux Hint https://ift.tt/3gp86Ob




0 Comments