How To Calculate Matrices in Python Without NumPy

The vertical series of objects in a Python matrix is generally known as the “columns,” whereas the horizontal series of things is referred to as the “rows.” Like a nested list, the rows and columns were placed on top of one another. If a matrix has “k” rows and “m” columns, and if “k” and “m” are positive integers, the order of such a matrix object is determined by “k-by-m”.

A matrix can hold strings, numbers, and other data kinds of objects. In a matrix, data is stacked in both columns and rows. A key data structure supporting computations in science and math is the matrix. Since Python does not provide a built-in type for a matrix object, we treat either list among lists or even a nested list as a matrix.

How Matrices in Python Work

Data is written in a two-dimensional array to generate a matrix. The procedure is as follows:

[[1 3 5 7 9 ]
  [2 4 6 8 10]  
  [0 8 7 4]]

It has a 3 by 5 matrix as its display. Hence, its size is 3 by 5. The data inside this matrix consists of objects of either the data type integer. The top row, Row1, has the values 1, 3, 5, 7, and 9, whereas Row2, along with Row3, has the values (2, 4, 6, 8) and respectively (0, 8, 7, 4). Column1 contains values of (1, 2, 0) as well as Column2 has values of (3, 4, 8) and so on.

Python enables us to store all data in a matrix with two dimensions. We can add matrices, multiply them, transpose them, and execute other operations on a matrix. Utilizing arrays, we may build a Python matrix and use it similarly. Let’s talk about different examples of Python Matrices.

Python Matrix Addition

We will take the two matrices and add them to iterate through them using a nested for loop.

matrix1 = [[2, 4, 1],    
           [4, 1, 5],    
           [3, 6, 7]]    
   
matrix2 = [[4, 2, -1],    
           [5, 6, -3],    
           [0, -4, 3]]    
   
matrix3  = [[0,1,0],    
            [1,0,0],    
            [0,0,1]]  
 
matrix4  = [[0,0,1],    
            [0,1,0],    
            [1,0,0]]  

matrices_length = len(matrix1)

for row in range(len(matrix1)):    
    for column in range(len(matrix2[0])):    
        matrix4[row][column] = matrix1[row][column] + matrix2[row][column] + matrix3[row][column]  

print("The sum of the matrices is = ", matrix4)

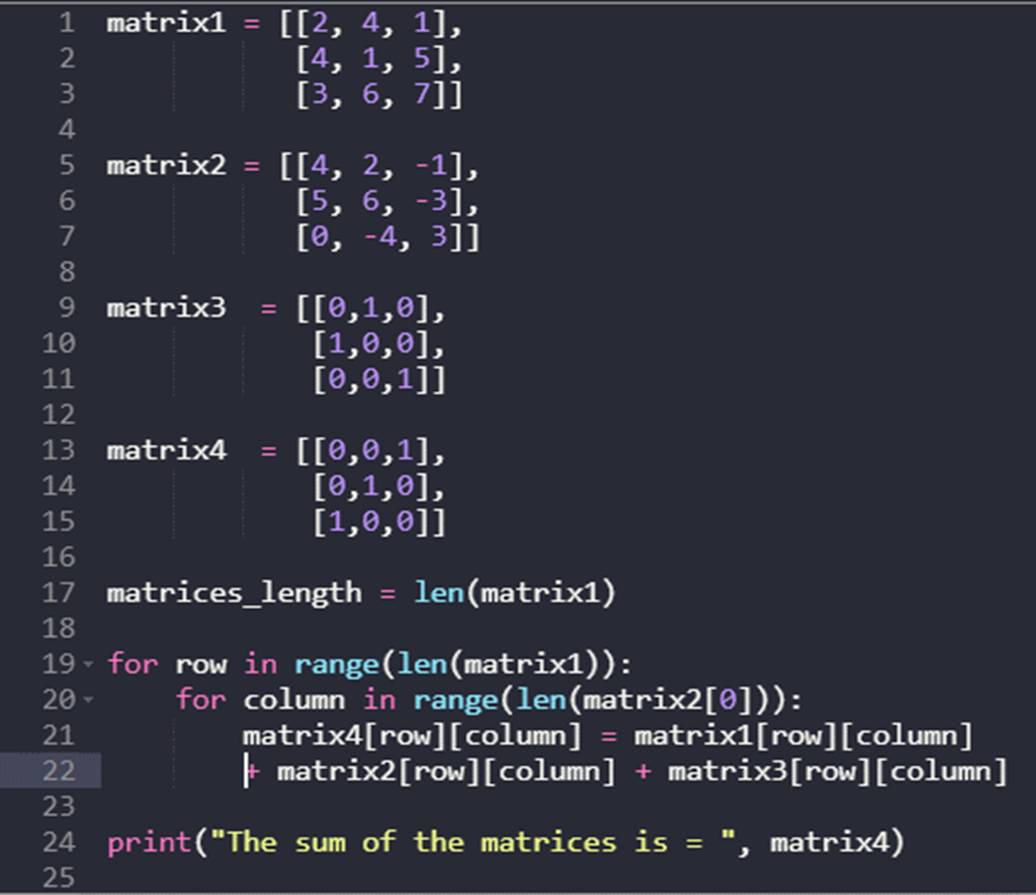
Initially, rather than using NumPy, we directly built three matrices having order 3-by-3. We specified the order or length of matrix 1 as len() function and others, respectively. Using nested loops, first, the three matrices were added. The total of the three matrices was then specified as matrix 4, and we used the print() function to display the results.

Transpose a Matrix in Python

By swapping the elements of the matrix’s columns and rows, we could transpose them. Using different examples, we will demonstrate how to obtain a transpose of a matrix using Python without NumPy.

A matrix’s transposition is represented by the symbol At. For instance, suppose we have a matrix “A” having the order of:

3-by-2

Then the transpose of A is:

2-by-3 matrix

Calculating Transpose of a Matrix With the Help of a Nested Loop

The nested loop may be used to repeatedly iterate through the columns and the rows of even a nested list. Insert the element in the “ith” row and the “jth” column of matrix F alongside the “jth” row and “ith” column of matrix “F^T” to obtain the transpose of the matrix. “F^T” will be a 2-by-3 matrix assuming “F” is a 3-by-2 matrix.

F = [[2, 3],
[5, 7],
[8, 1]]

F_T = [[0, 0, 0],
       [0, 0, 0]]

for q in range(len(F)):
    for w in range(len(F[0])):
        F_T[w][q] = F[q][w]

for q in F_T:
    print(q)

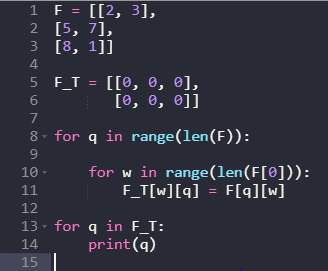
A transpose matrix of the original matrix and a matrix “F” with a 3-by-2 order is first created. The previous program uses nested “for” loops, continually iterated over each row and subsequently each column. At each iteration, we add an element from “F[q][w]” into “FT[w][q]”. Finally, we execute the print() method to depict the transpose.

Using a Nested List Comprehension to Find the Transpose of the Matrix

A nested list is produced when a list comprehension is performed inside of another list comprehension. The following is the syntax for comprehending nested lists:

new_list = [[expr. for a list item] for a list item]

Likewise, we may obtain a matrix’s transpose using nested list comprehension in such a nested loop approach.

J = [[1, 3],
[4, 6],
[9, 2]]

J_T = [[J[v][c] for v in range(len(J))] for c in range(len(J[0]))]

for c in J_T:
    print(c)

We start by creating matrix “J”, having the order 3-by-2. The nested list comprehension in the code preceding loops over the matrix’s members once at a time and inserts the elements of “J[v]” somewhere at location “J_T[v]”. The matrix’s columns are iterated throughout the first part of such nested list comprehension, while its rows are repeated in the second column.

Multiplication of Two Matrices in Python

The binary process of multiplying matrices creates the matrix using two matrices. Utilizing nested loops and list comprehension, we may multiply matrices in Python.

The first matrix’s column and second-row count must match to accomplish matrix multiplication. The matrix we got at the end due to matrix multiplication will consist of the same order as the original matrix. An illustration of matrix multiplication is shown below.

Using Nested List to Find Multiplication of Matrix

A matrix may be created in Python as more than just a nested list, a kind of list inside a list. A row of a matrix corresponds to every value of a nested list. Let’s see an instance of a nested loop utilized to multiply two matrices.

N = [[9, 1, 7],
[3, 5, 6],
[4, 7, 8]]

M = [[2, 3, 5, 6],
[8, 9, 1, 2],
[4, 5, 9, 3]]

result = [[0, 0, 0, 0],
[0,0,0,0],
[0,0,0,0]]

for u in range(len(N)):
    for o in range(len(M[0])):
        for p in range(len(M)):
            result[u][o] += N[u][p] * M[p][o]
for d in result:
    print(d)

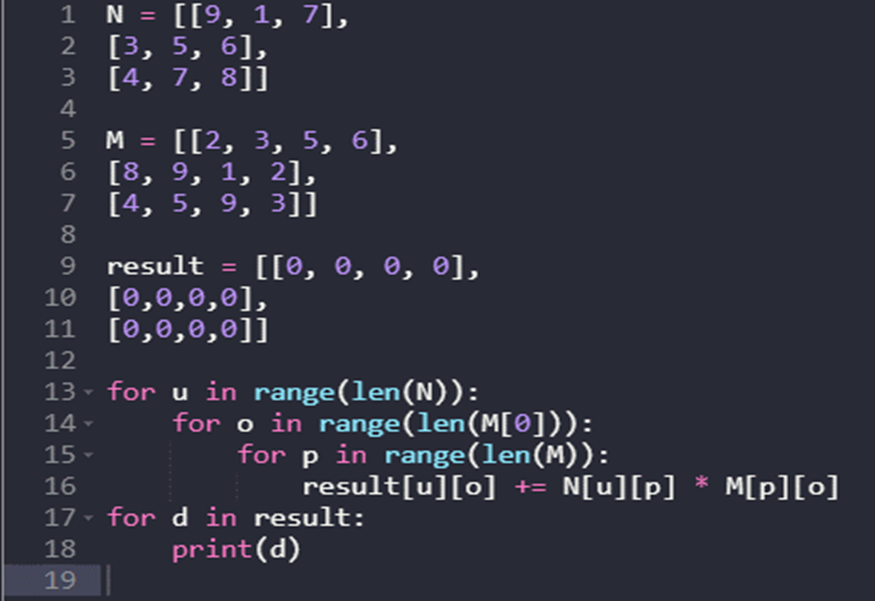
In this example, we’ll use nested loops to execute a program that multiplies two matrices, but before we do so, we’ll generate two matrices, “N” and “M”, that are 3-by-3 and 3-by-4 in order, respectively, as well as a third matrix that has order 3-by-4. Next, we go through an iteration process where we utilize the elements of the rows in “N”, the columns in “M”, and the rows in “M”. We applied the print statement to display the multiplication of the defined matrices.

Utilizing Nested List Comprehension to Find Multiplication of Matrices

Nested list comprehension is the process of performing a list comprehension together within list comprehension, resulting in some kind of a nested list

Syntax:

# new_list = [[expr. for a list item] for a list item]

Likewise, with that same nested loop approach, we can also perform the multiplication of two matrices by using the method of nested list comprehension easily.

E = [[8, 1, 3],
[8, 7, 3],
[7, 3, 5]]

R = [[2, 3, 6, 8],
[9, 8, 5, 3],
[1, 3, 8, 9]]

result = [[sum(f*g for f,g in zip(E_row, R_col)) for R_col in zip(*R)] for E_row in E]

for z in result:
    print(z)

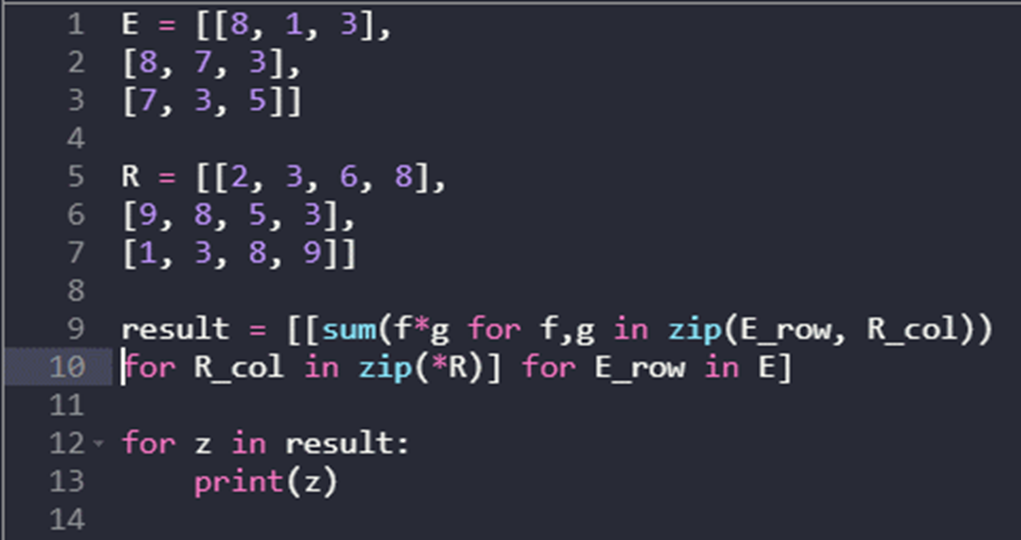
To get the total of the products of each row-by-column multiplication, we iterate over the columns inside matrix “R” and the rows inside the matrix “E” in the program. To obtain the columns of matrix “R”, we utilize the zip() method. We require the elements of the row in the “E” matrix as the second component of a nested list comprehension to compute the sum of products for each row inside this nested list. In the end, the print statement will be employed.

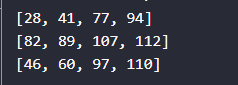
Conclusion

In this guide, we’ve seen a few alternative ways to manually compute matrix addition, multiplication, and transposition rather than NumPy. These approaches include nested lists as well as comprehension of nested lists. Additionally, several programs are presented to demonstrate how these approaches can be utilized and work differently with addition, multiplication, and transposition of a matrix.

from https://ift.tt/F0n8fwG