matrix = [ [1, 2, 4], [31, 17, 15] ]
The list inside the list above is a row, and every element inside the list is called a column. So, in the above example, we have two rows and three columns [2 X 3].
And also, indexing of the Python starts from zero.
The transpose of a matrix means where we change the rows to columns or columns to rows.
Let’s discuss different kinds of methods to do matrix transpose.
Method 1: Transpose a NumPy Matrix transpose()
The first method which we are going to discuss is the Numpy. The Numpy mostly deals with the array in Python, and for the transpose, we called the method transpose ().
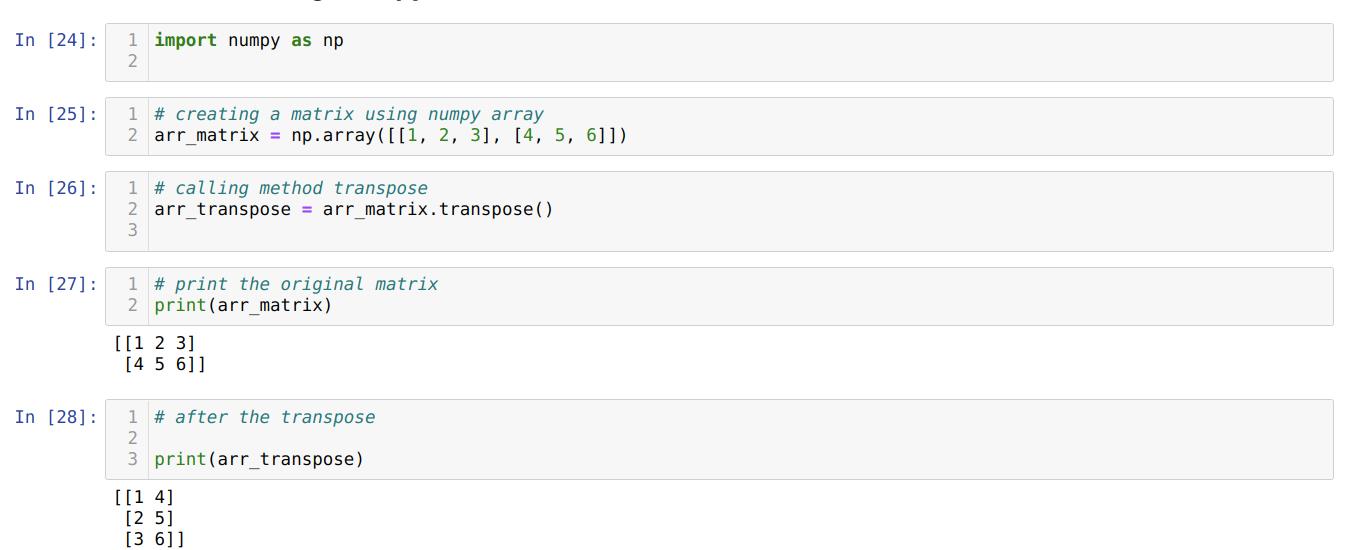
In cell number [24]: We import the module NumPy as np.
In cell number [25]: We are creating a NumPy array with the name arr_matrix.
In cell number [26]: We call the method transpose() and use the dot operator with the arr_matrix we created before.
In cell number [27]: We are printing the original matrix (arr_matrix).
In cell number [28]: We are printing the transpose matrix (arr_transpose), and from the results, we found that our matrix is now transposed.
Method 2: Using the method numpy.transpose()
We can also transpose a matrix in Python using the numpy.transpose (). In that, we are passing the matrix into the transpose()method as a parameter.
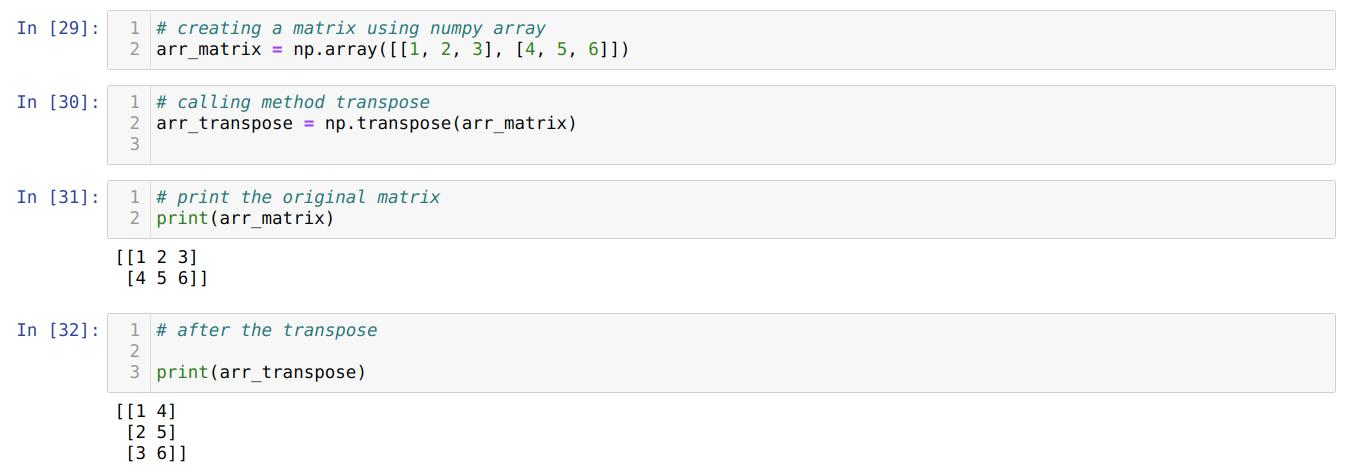
In cell number [29], we create a matrix using a NumPy array with the name arr_matrix.
In cell number [30]: We passed the arr_matrix to the transpose () method and store the results back to a new variable arr_transpose.
In cell number [31]: We are printing the original matrix (arr_matrix).
In cell number [32]: We are printing the transpose matrix (arr_transpose), and from the results, we found that our matrix is now transposed.
Method 3: Matrix Transpose using Sympy library
A Sympy library is another approach that helps us to transpose a matrix. This library is using symbolic mathematics to solve the problems of algebra.
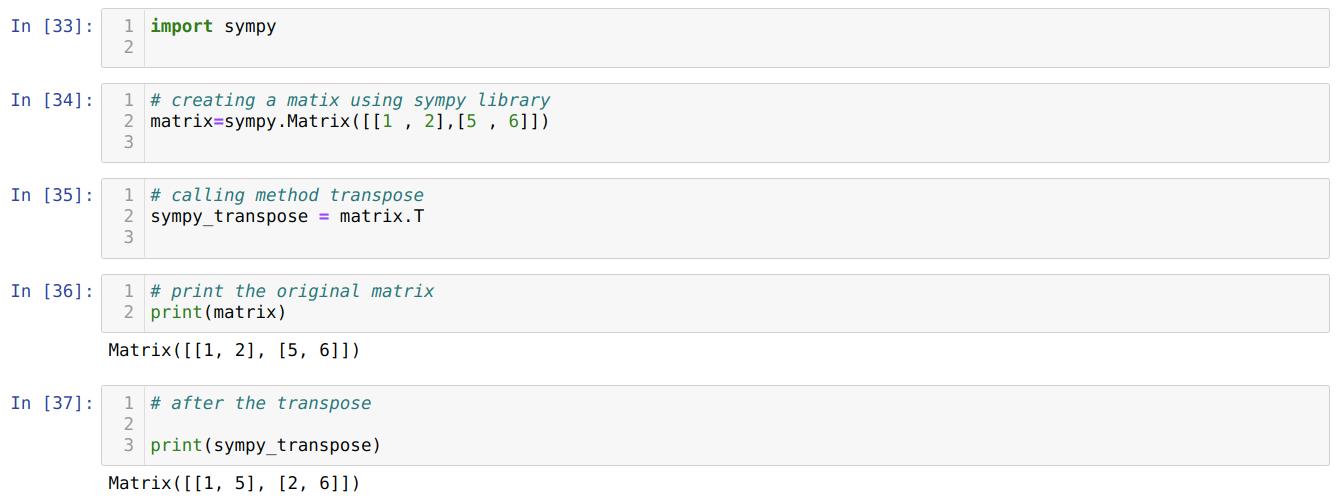
In cell number [33]: We import the Sympy library. It’s not coming along with the Python, so you have to install it explicitly to your system before using this library; else, you will get errors.
In cell number [34]: We create a matrix using the sympy library.
In cell number [35]: We call the transpose (T) with the dot operator and store the results back to a new variable sympy_transpose.
In cell number [36]: We are printing the original matrix (matrix).
In cell number [37]: We are printing the transpose matrix (sympy_transpose), and from the results, we found that our matrix is now transposed.
Method 4: Matrix transpose using nested loop
The matrix transpose without any library in Python is a nested loop. We are creating a matrix and then creating another matrix of the same size as the original matrix to store the results back after transpose. We do not do a hard code of the results matrix because we do not know the dimension of the matrix in the future. So, we are creating the result matrix size using the original matrix size itself.
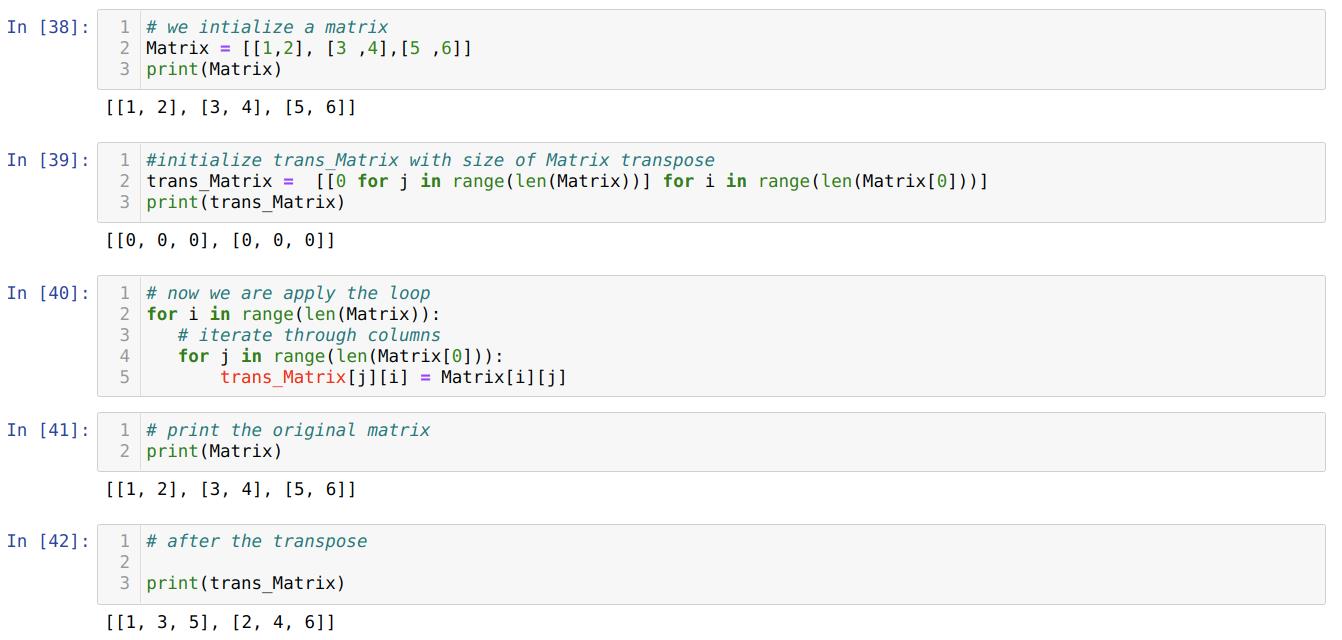
In cell number [38]: We create a matrix and print that Matrix.
In cell number [39]: We use some pythonic ways to find out the dimension of the transpose matrix using the original matrix. Because if we do not do this, then we have to mention the dimension of the transpose matrix. But with this method, we do not care about the dimensions of the matrix.
In cell number [40]: We run two loops. One upper loop is for the rows and the nested loop for the column-wise.
In cell number [41]: We are printing the original matrix (Matrix).
In cell number [42]: We are printing the transpose matrix (trans_Matrix), and from the results, we found that our matrix is now transposed.
Method 5: Using the list comprehension
The next method which we are going to discuss is the list comprehension method. This method is similar to the normal Python using nested loops but in a more pythonic way. We can say that we have a more advanced way to solve the matrix transpose in a single line of code without using a library.
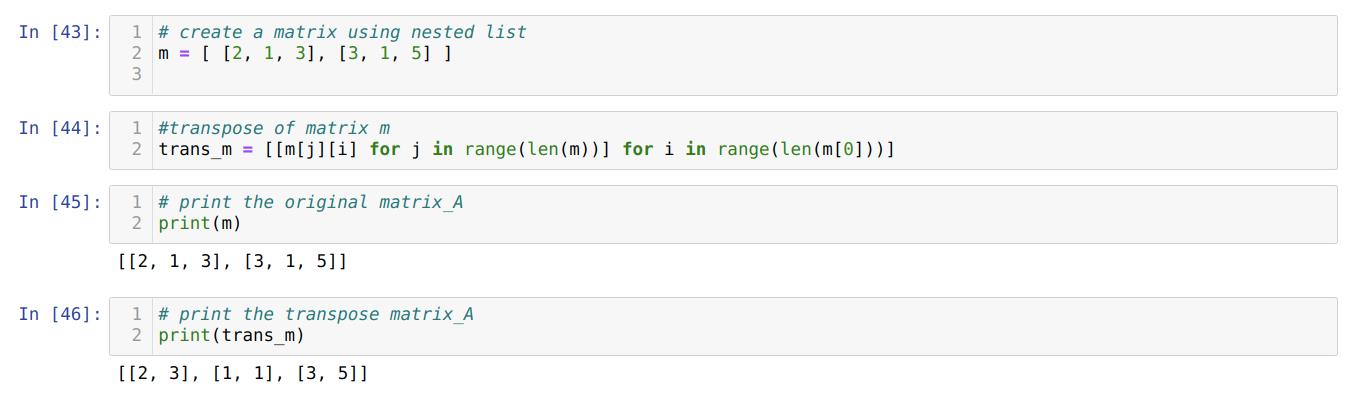
In cell number [43]: We create a matrix m using the nested list.
In cell number [44]: We use the nested loop as we discuss in the previous but here in a single line and also no need to mention opposite index[j][i], as we did in the previous nested loop.
In cell number [45]: We are printing the original matrix (m).
In cell number [42]: We are printing the transpose matrix (trans_m), and from the results, we found that our matrix is now transposed.
Method 6: Transpose a matrix using pymatrix
The pymatrix is another lightweight library for matrix operations in Python. We can also do the transpose using the pymatrix.
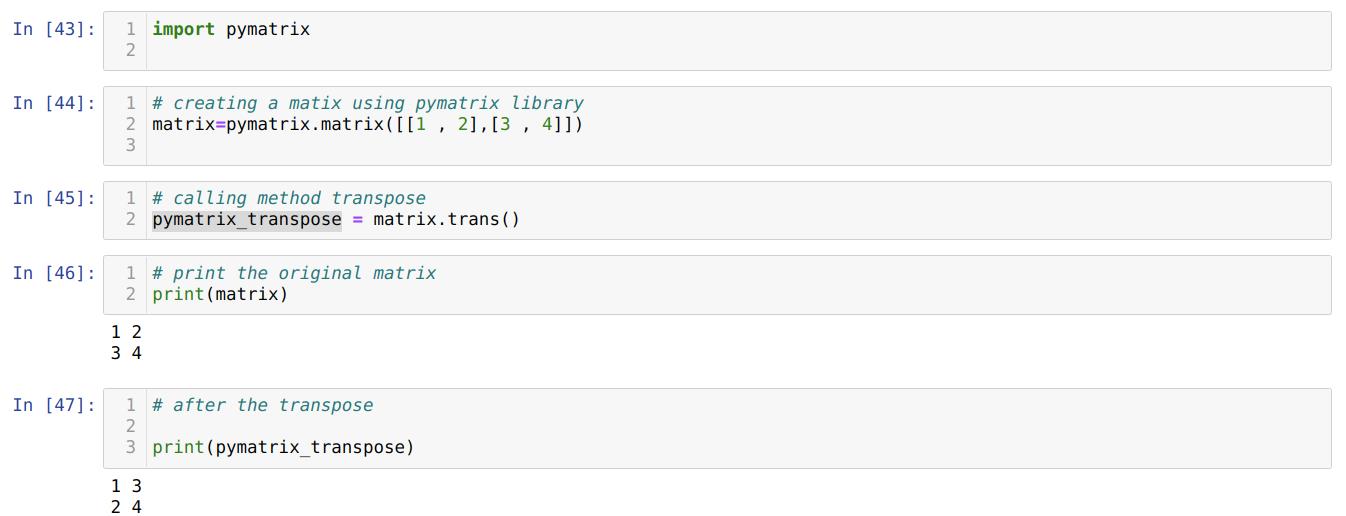
In cell number [43]: We import the pymatrix library. It’s not coming along with the Python, so you have to install it explicitly to your system before using this library; else, you will get errors.
In cell number [44]: We create a matrix using the pymatrix library.
In cell number [45]: We call the transpose (trans()) with the dot operator and store the results back to a new variable pymatrix_transpose.
In cell number [46]: We are printing the original matrix (matrix).
In cell number [47]: We are printing the transpose matrix (pymatrix_transpose), and from the results, we found that our matrix is now transposed.
Method 7: Using the zip method
The zip is another method to transpose a matrix.
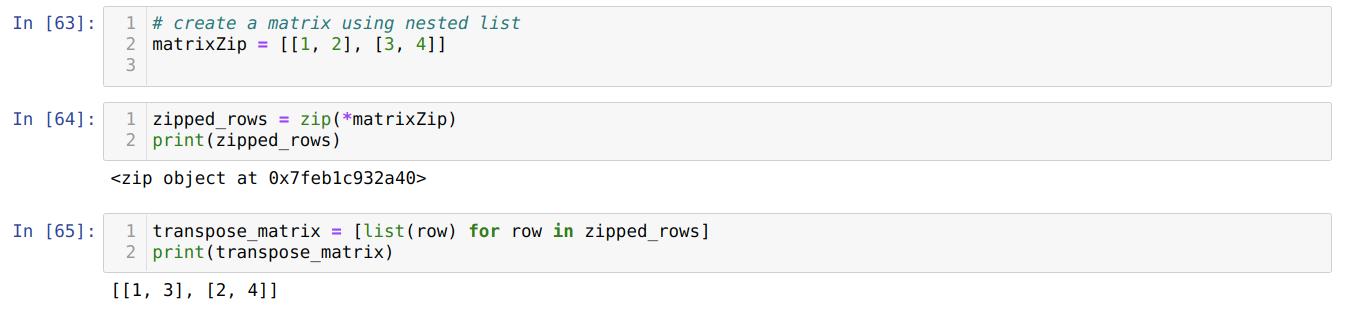
In cell number [63]: We created a new matrix using the list.
In cell number [64]: We passed the matrix to the zip with the * operator. We call each row and then convert that row to a new list that becomes the matrix’s transpose.
Conclusion: We have seen different kinds of methods that can help us in the matrix transpose. In which some of the methods use the Numpy array and list. We have seen that creating the matrix using the nested list is very easy as compared to the Numpy array. We have also seen some new libraries like pymatrix and sympy. In this article, we try to mention all the transpose methods which the programmer uses.
from Linux Hint https://ift.tt/3xF0DDH




0 Comments